（Dijkstra 算法）有权有向图求一个点到其它所有点最短路径

思想

Dijkstra算法其实是贪婪算法，贪婪算法一般分阶段求解一个问题，在每个阶段它都把出现的当作是最好的去处理。

Dijkstra算法按阶段进行，正像无权最短路径算法一样。

1. 在每个阶段，Dijkstra 算法选择一个顶点v，它在所有 unknown 顶点中具有最小的dv。同时算法声明从s到v的最短路径是 known 的。
2. 阶段的其余部分由dw值的更新工作组成。

若顶点v能提供一条更短路径，则我们本质上降低了dw的值。当dw的新值dv+cvw是一个改进的值时我们就置dw=dv+cvw。

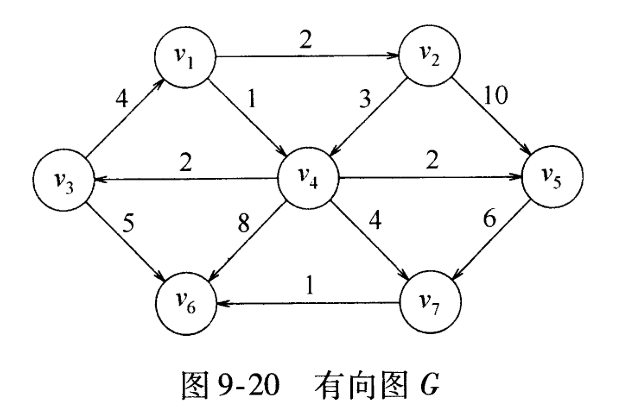
• 举个例子，s起始点是v1，v是v7，w是v6。之前到达v6是走v1->v4->v6。
• 现在走v1->v4->v7->v6时，dv+cvw=5+1，dw是1+8。由于dv+cvw<dw，所以v6的dw改为6，上一个路径变成走v7。

步骤

1. 定义邻接表、初始化距离
2. 定义一个变量看是否所有点已经know
3. 有未知的点就循环处理
   1. 找最小距离且未知顶点
   2. 设置点为已经know，后面如果是已经know，不再改变距离路径
   3. 更新当前点指向的点的距离，路径
   4. 检测isAllKnow

代码

import java.util.ArrayList;
import java.util.List;

public class WeightedGraph {
    private static final int INFINITY = 999999999;

    static void printPath(Vertex v) {
        if (v.path != null) {
            printPath(v.path);
            System.out.println("到");
        }
        System.out.println(v);
    }

    /**
     * 把邻接矩阵转邻接表
     *
     * @param matrix 图的邻接矩阵,点从0开始
     */
    private static List<Vertex> adjMatrix2List(int[][] matrix) {
        //1. 定义点的列表，要初始化好入度，指向的点，值
        List<Vertex> vertexList = new ArrayList<>();

        //2. 遍历每一个点，找其所有adjVertex
        for (int i = 0; i < matrix.length; i++) {
            int[] edges = matrix[i];
            Vertex vertex = new Vertex(i);
            // example:   {0,0,3,4,9}
            for (int j = 0; j < edges.length; j++) {
                //i点有指向这个j点
                if (edges[j] != 0) {
                    AdjV adjV = new AdjV(j);
                    adjV.weight = edges[j];
                    vertex.adj.add(adjV);
                }
            }
            vertexList.add(vertex);
        }

        return vertexList;
    }

    public static void dijkstra(int[][] matrix, int s) {
        // 1. 定义邻接表、初始化距离
        List<Vertex> vertexList = adjMatrix2List(matrix);
        int i = 1;
        for (Vertex v :
                vertexList) {
            v.dist = INFINITY;
            v.known = false;
        }

        vertexList.get(s).dist = 0;

        // 2. 定义一个变量看是否所有点已经know
        boolean isAllVKnow = false;

        // 3. 有未知的点就循环处理
        while (!isAllVKnow) {

            // 1. 找最小距离且未知顶点
            Vertex v = null;
            int minDist = INFINITY;
            for (Vertex vertex :
                    vertexList) {
                if (vertex.dist < minDist && !vertex.known) {
                    v = vertex;
                    minDist = vertex.dist;
                }
            }

            // 2. 设置点为已经know，后面如果是已经know，不再改变距离路径
            v.known = true;

            // 3. 更新当前点指向的点的距离，路径
            for (AdjV adjV : v.adj) {
                Vertex w = vertexList.get(adjV.v);
                if (!w.known) { // 点是不知道的
                    int cvw = adjV.weight;

                    // 更短就更新值和路径
                    if (v.dist + cvw < w.dist) {
                        w.dist = v.dist + cvw;
                        w.path = v;
                    }
                }
            }

            // 4. 检测isAllKnow
            isAllVKnow = true;
            for (Vertex vertex : vertexList) {
                if (!vertex.known) {
                    isAllVKnow = false;
                    break;
                }
            }
        }

        // 打印看看
        for (Vertex v :
                vertexList) {
            System.out.println("这时打印的点是： v" + (v.value) + ", 距离：" + v.dist);
            printPath(v);
        }

    }


    private static class Vertex {
        public List<AdjV> adj;
        public boolean known;
        public int dist;
        public Vertex path;
        public int value;

        public Vertex(int value) {
            this.adj = new ArrayList<>();
            this.known = false;
            this.path = null;
            this.value = value;
        }

        @Override
        public String toString() {
            return "Vertex{" +
                    "value=" + value +
                    ", dist=" + dist +
                    ", path=" + path +
                    '}';
        }
    }

    /**
     * 存指向的点的序号
     * 和权重
     */
    private static class AdjV {
        int v;// 几号点
        int weight;

        public AdjV(int v) {
            this.v = v;
        }
    }
}

测试

public class Main {
    public static void main(String[] args) {

        int[][] matrix = {
                {0, 2, 0, 1, 0, 0, 0,},
                {0, 0, 0, 3, 10, 0, 0,},
                {1, 0, 0, 0, 0, 5, 0,},
                {0, 0, 2, 0, 2, 8, 4,},
                {0, 0, 0, 0, 0, 0, 6,},
                {0, 0, 0, 0, 0, 0, 0,},
                {0, 0, 0, 0, 0, 1, 0,},
        };
        WeightedGraph.dijkstra(matrix, 0);
    }
}

打印出来的点从v0开始，点的序号是value