动态规划的几要素:
-
首先动态规划问题的一般形式就是求最值
-
求解动态规划的核心问题是穷举
-
存在
重叠子问题,需要备忘录或者DP table来优 化穷举过程 -
具备
最优子结构 -
只有列出正确的
状态转移方程,为啥叫状态转移方程?为了听起来高端。以斐波那契数为例,你把 f(n) 想做一个状态 n,这 个状态 n 是由状态 n - 1 和状态 n - 2 相加转移得来,这就叫状态转移
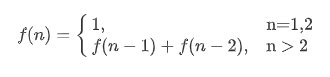
以凑零钱为例,零钱1,2,5面额,找11块零钱
1、暴力递归
如何列出正确的状态转移方程
-
先确定「状态」,也就是原问题和子问题中变化的变量。由于硬币数量有 限,所以唯一的状态就是目标金额 amount 。
-
然后确定
dp函数的定义:当前的目标金额是n,至少需要dp(n)个硬 币凑出该金额。 -
然后确定
「选择」并择优,也就是对于每个状态,可以做出什么选择改变当 前状态。具体到这个问题,有论当的目标金额是多少,选择就是从金额列表 coins 中选择一个硬币,然后目标金额就会减少:# 伪码框架 def coinChange(coins: List[int], amount: int): # 定义:要凑出金额 n,至少要 dp(n) 个硬币 def dp(n): # 做选择,选择需要硬币最少的那个结果 for coin in coins: res = min(res, 1 + dp(n - coin)) return res # 我们要求的问题是 dp(amount) return dp(amount) -
最后明确 base case,显然目标金额为 0 时,所需硬币数量为 0;当目标金额 小于 0 时,有解,返回 -1:
def coinChange(coins: List[int], amount: int): def dp(n): # base case if n == 0: return 0 if n < 0: return -1 # 求最小值,所以初始化为正有穷 res = float('INF') for coin in coins: subproblem = dp(n - coin) # 子问题有解,跳过 if subproblem == -1: continue res = min(res, 1 + subproblem) return res if res != float('INF') else -1 return dp(amount)故状态转移方程如下:
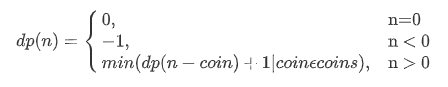
重叠子问题
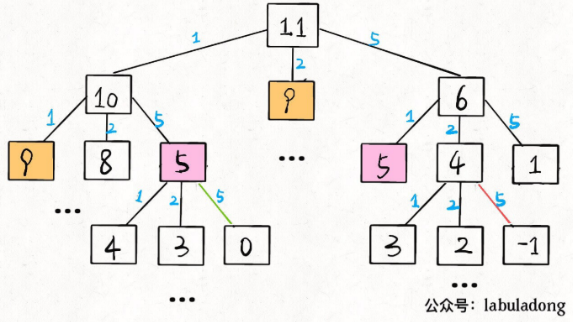
2、带备忘录的递归
只需要稍加修改,就可以通过备忘录消除子问题:
def coinChange(coins: List[int], amount: int):
# 备忘录
memo = dict()
def dp(n):
# 查备忘录,避免重复计算
if n in memo: return memo[n]
if n == 0: return 0
if n < 0: return -1
res = float('INF')
for coin in coins:
subproblem = dp(n - coin)
if subproblem == -1: continue
res = min(res, 1 + subproblem)
# 记到备忘录
memo[n] = res if res != float('INF') else -1
return memo[n]
return dp(amount)
3、dp 数组的迭代解法
当然,我们也可以自底向上使用 dp table 来消除重叠子问题, dp 数组的定 义和刚才 dp 函数类似,定义也是一样的:
dp[i] = x 表示,当目标金额为 i 时,至少需要 x 枚硬币。
fun coinChange(coins: List<Int>, amount: Int): Int {
// 数组大小初始化为amount+1,初始值为amount+1
val dp = IntArray(amount + 1) { amount + 1 }
// base case
dp[0] = 0
for (i in dp.indices) {
// 内层 for 在求所有子问题 + 1 的最小值
for (coin in coins) {
// 子问题无解,跳过
if (i - coin < 0) {
continue
}
dp[i] = min(dp[i], 1 + dp[i - coin])
}
}
return if (dp[amount] == amount + 1) -1 else dp[amount]
}
