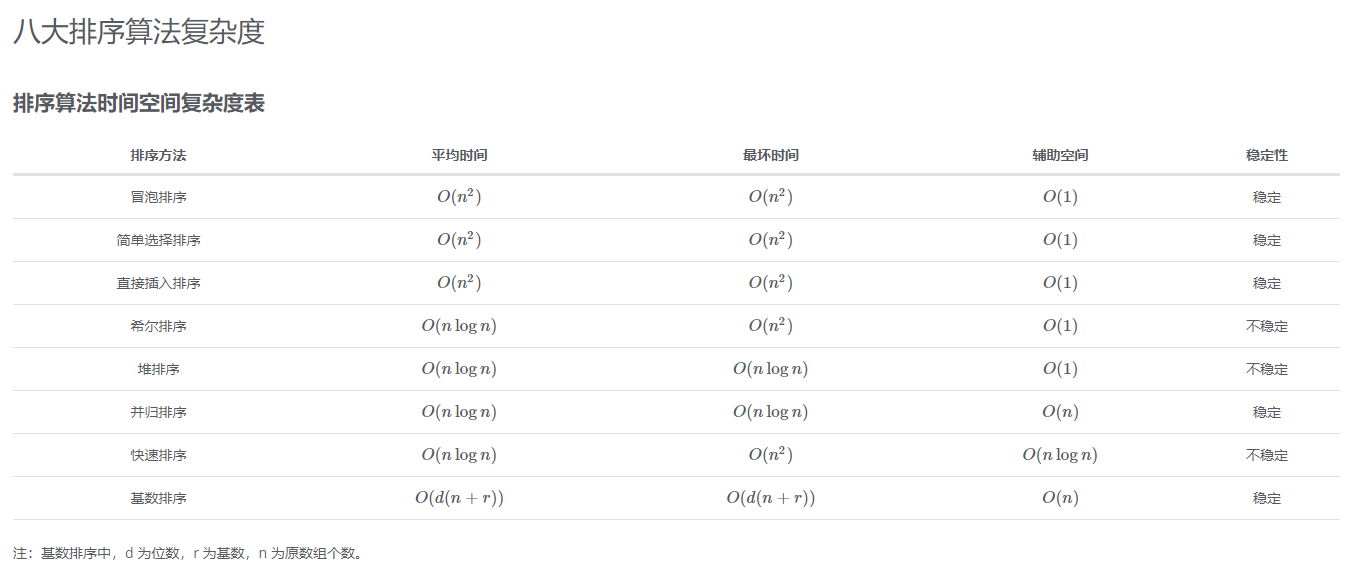
各种排序算法
1. 直接插入排序 (Insert Sort)
思想
- 当插入第
i (i >= 1)个对象时, 前面的V[1], V[2], …, V[i-1]已经排好序。 - 这时, 用V[i]的排序码与
V[i-1], V[i-2], …的排序码顺序进行比较, 找到插位置即将V[i]插入, 原来位置上的对象向后顺移。
图解
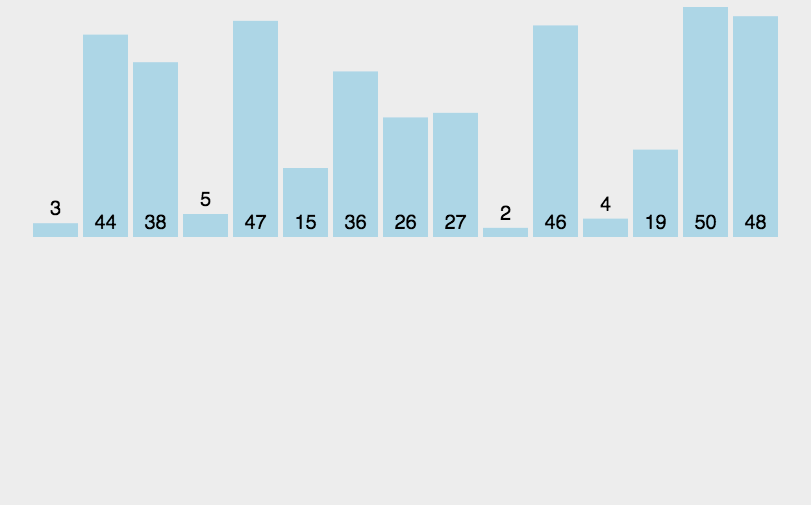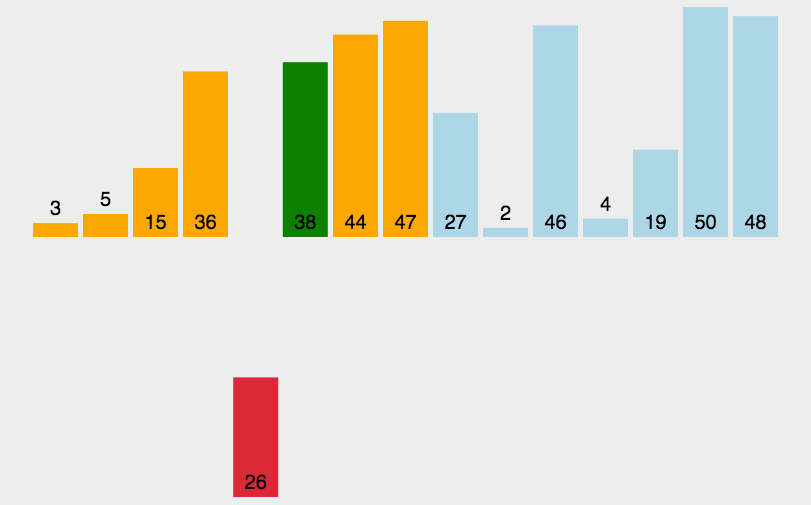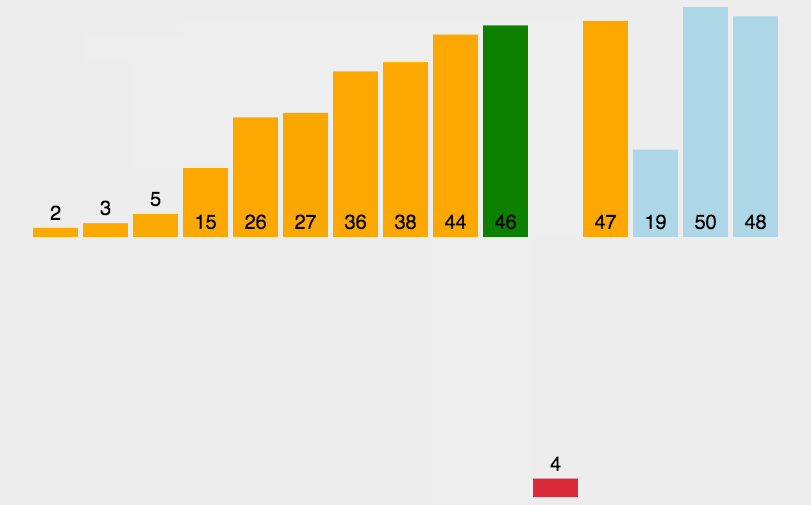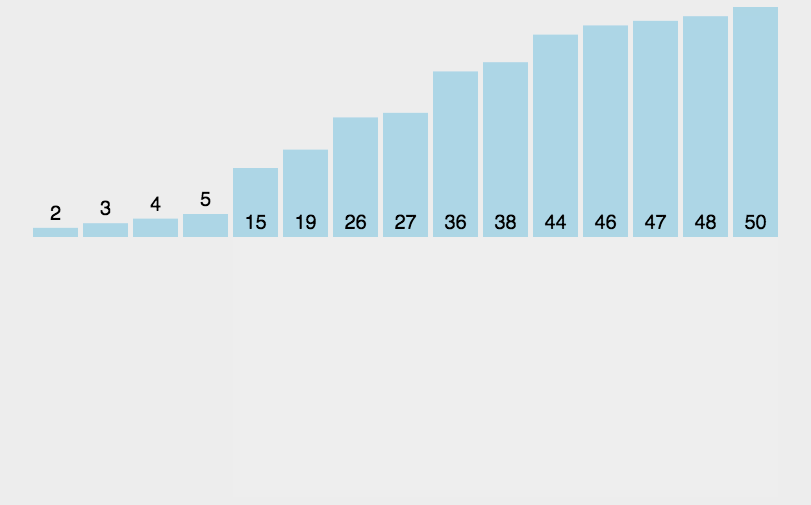
2. 折半插入排序 (Binary Insertsort)
思想
- 设在顺序表中有一 个对象序列
V[0], V[1], …, V[n-1]。 - 其中,
V[0], …, V[i-1]是已经排好序的对象。 - 在插入
V[i]时, 利用折半搜索法寻找V[i]的插入位置。
3. 希尔排序
思想
它通过比较相距一定间隔的元素来工作;各趟比较所用的距离随着算法的进行而减小,直到只比较相邻元素的最后一趟排序为止。
由于这个原因,希尔排序有时也叫作缩减增量排序
图解
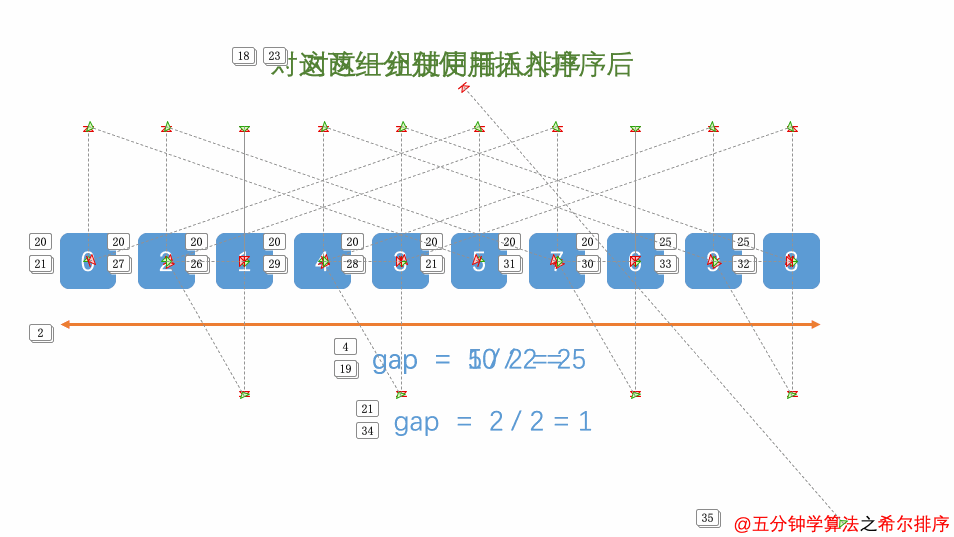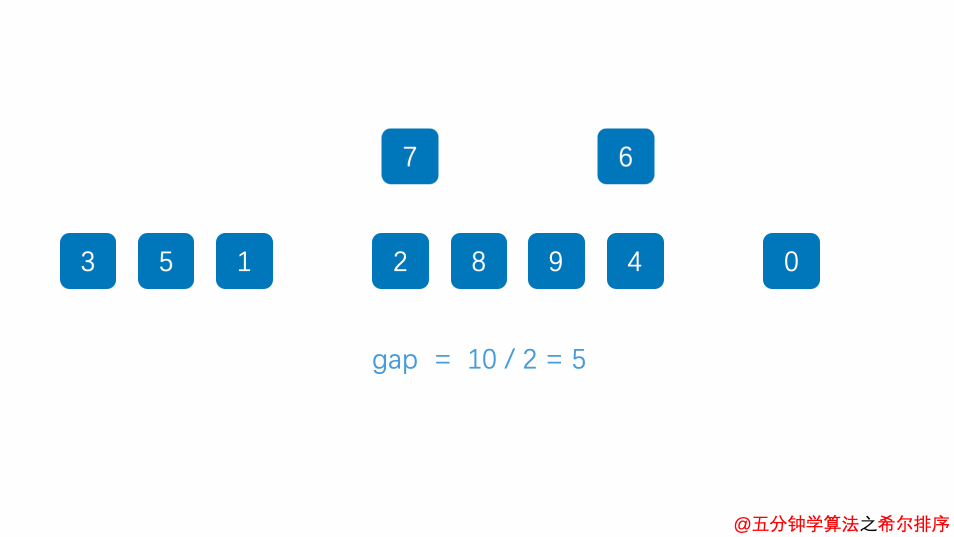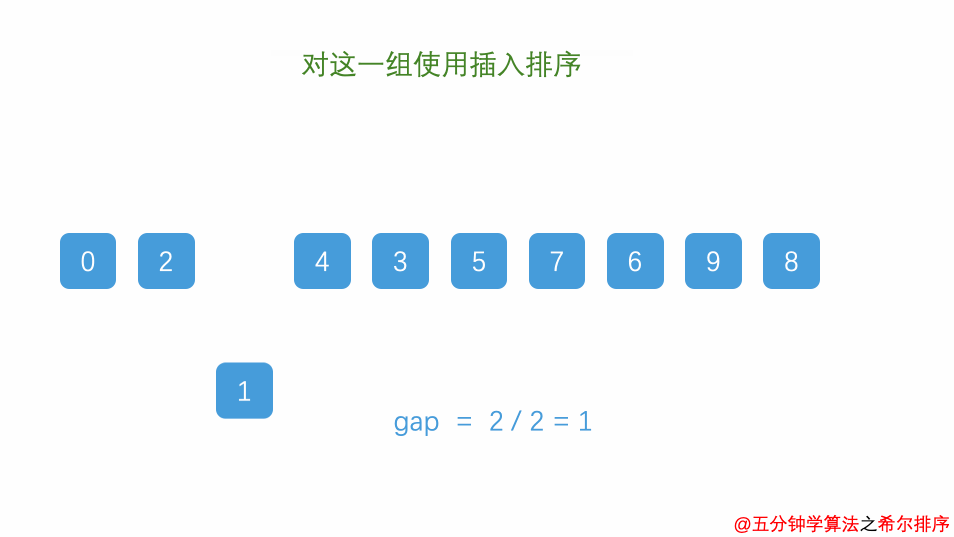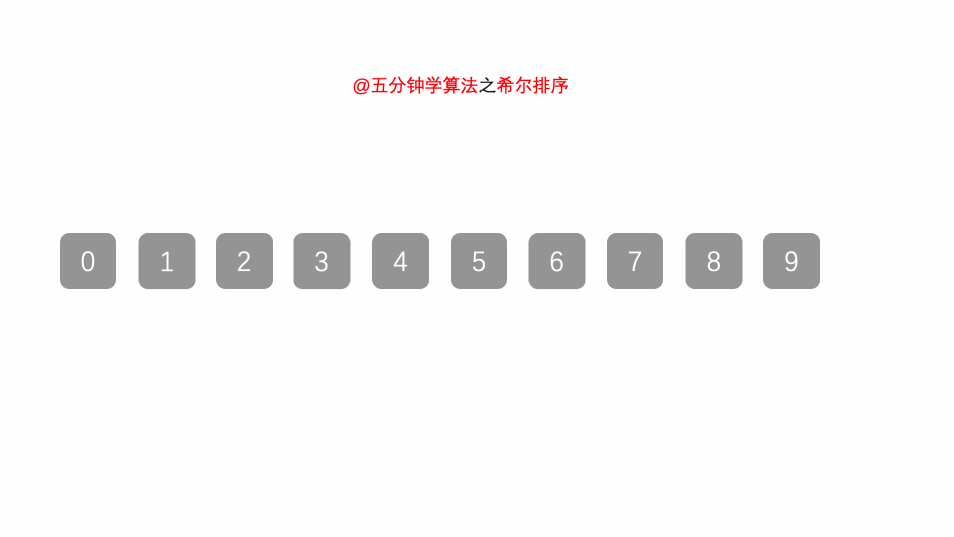
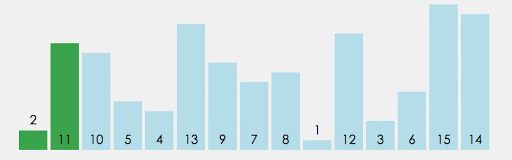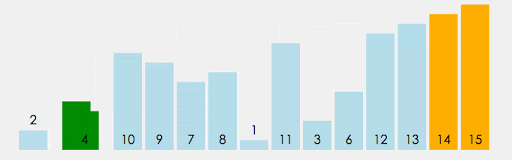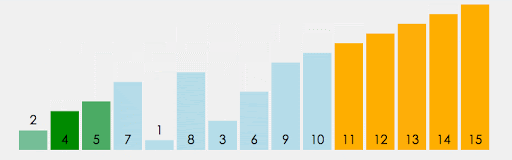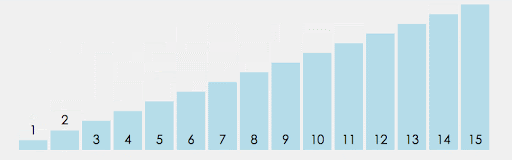
4. 冒泡排序 (Bubble Sort)
思想
- 基本方法设待排序对象序列中的对象个数为n。
- 一般地,第i趟起泡排序从1到n-i+1依次比较相邻两个记录的关键字,如果发生逆序,则交换之。
- 其结果是这n-i+1个记录中,关键字最大的记录被交换到第n-i+1的位置上,最多作n-1趟。
5. 快速排序 (Quick Sort)
思想
基本思想是任取待排序对象序列中的某个对象(例如取第一个对象)作为基准,按照该对象的排序码大小,将整个对象序列划分为左右两个子序列:
- 左侧子序列中所有对象的排序码都小于或等于基准对象的排序码
- 右侧子序列中所有对象的排序码都大于基准对象的排序码
- 基准对象则排在这两个子序列中间(这也是该对象最终应安放的位置)。
- 然后分别对这两个子序列重复施行上述方法,直到所有的对象都排在相应位置上为止。
- 基准对象也称为枢轴(或支点)记录。
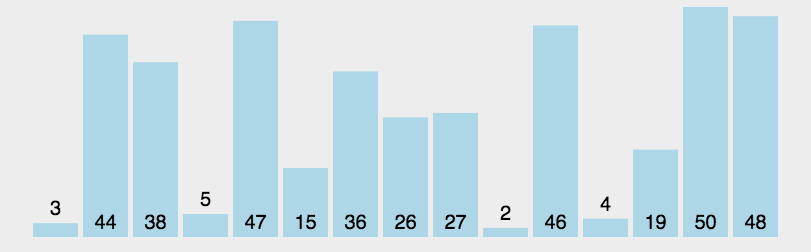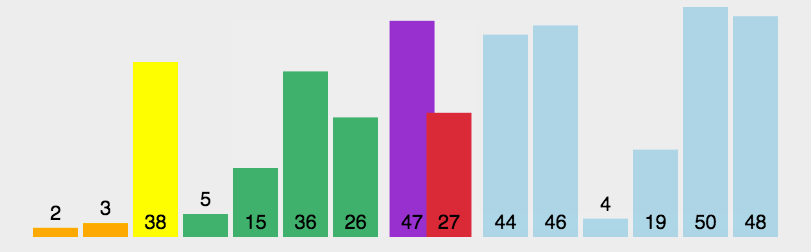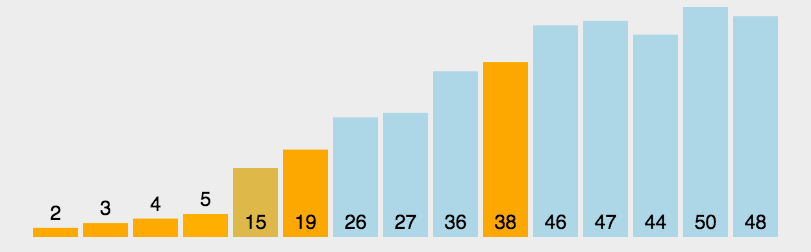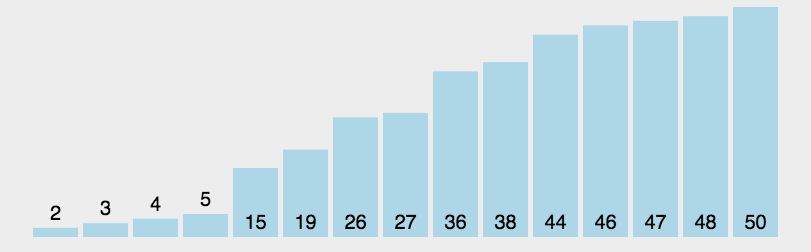
6. 直接选择排序 (Select Sort)
思想
- 在一组对象Vi]~VIn-1]中选择具有最小排序码的对象;
- 若它不是这组对象中的第一个对象,则将它与这组对象中的第一个对象对调)
- 在这组对象中剔除这个具有最小排序码的对象。在剩下的对象V[i+1]~VIn-1]中重复执行第①、②步,直到剩余对象只有一个为止。
7. 树形选择排序──锦标赛排序
思想
树形选择排序:是一种按照锦标赛的思想进行选择排序的方法.
- 对n个纪录进行两两比较,选出较小(大)。
- 对1中选出的较小(大)的,重复1,直到选出最小(大)的。
- 将选出的最小(大)的输出,并将其赋为最大(小)值。
重复1、2,直到n个纪录全部输出。
n个纪录用n个叶子结点表示,往上构成一棵完全二叉树,除叶子结点外,还要增加内部结点与根结点的辅助存贮空间n-1个
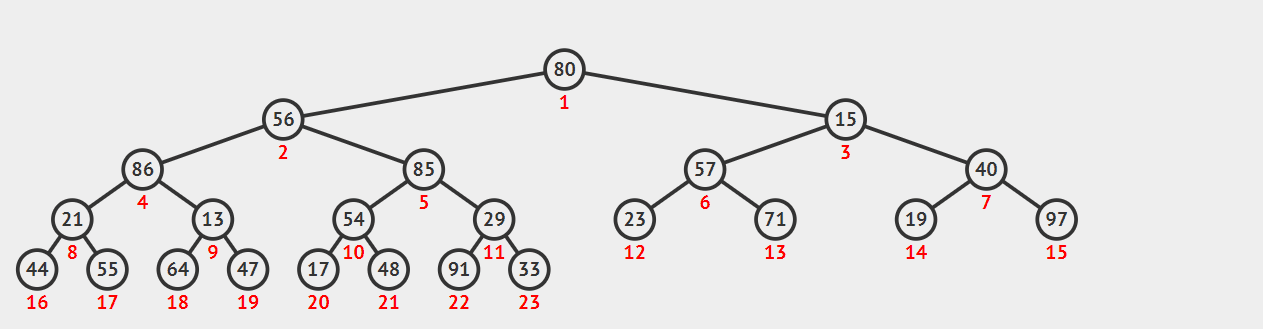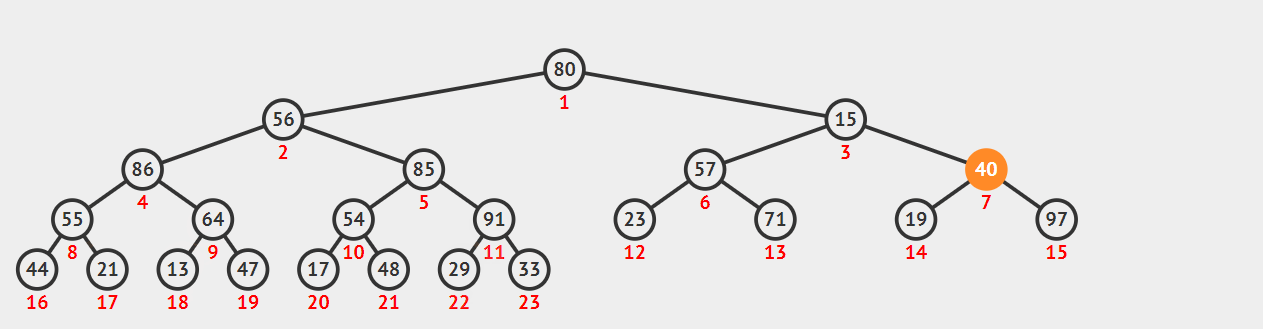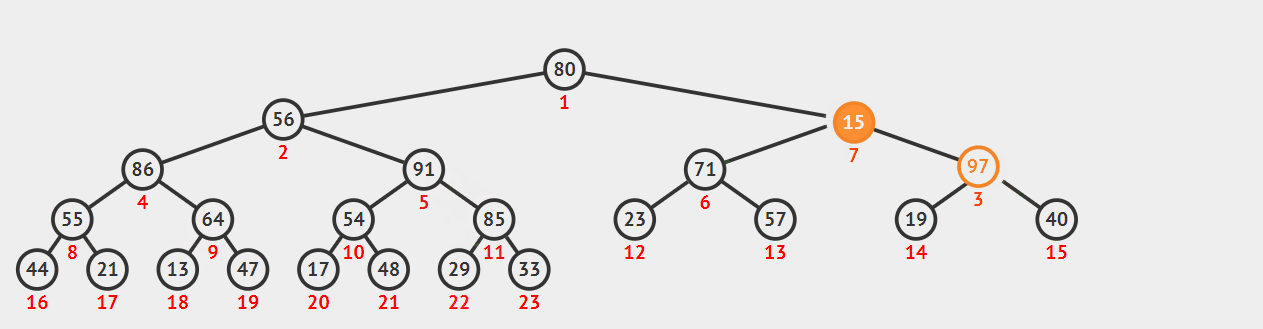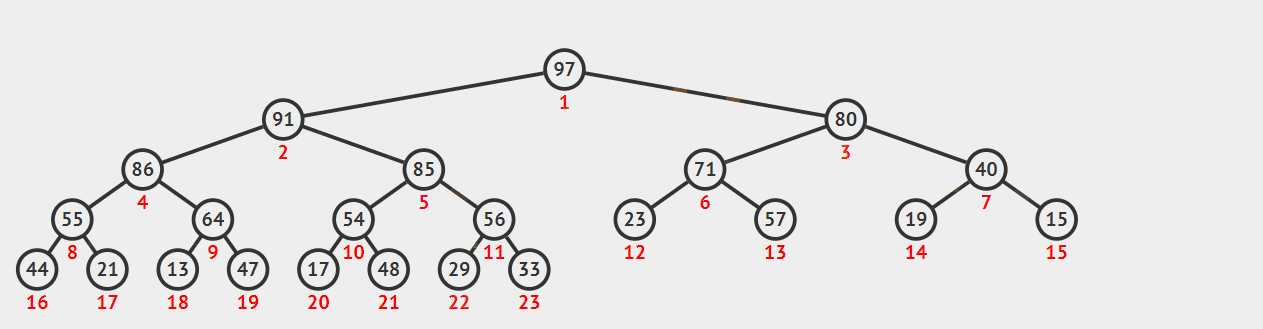
8. 堆排序( Heap sort )
思想
若在输出堆顶值之后,使得剩余n-1个元素的序列重又建成一个堆,则得到n个元素中的次小值。如此反复执行,便能得到一个有序序列。
- 建堆:用顺序结构存完全二叉树,n个元素只需n个结点
- 筛选:输出堆顶,即堆顶与堆的最后一个元素交换;再将剩余的元素自堆顶至叶子调整成堆。
9. 归并排序
思想
归并将两个或两个以上的有序表合并成一个新的有序表。
两路归并 (2-way merging)
原始序列initList[]中两个有序表
- initList[1] … initList[m]
- initList[m+1] … initList[n]
它们可归并成一个有序表, 存于另一对象序列mergedList的 l … n 中。
10.链式基数排序(LSD法)
思想
用多关键字排序思想对单关键字进行排序
多关键字排序:
- 依主,次,次次关键字,…,排序
单关键字排序:
- 按位把单关键字K看成由多个子关键字组成:
K=K1K2…Kd
各种排比较