堆排序

思想

若在输出堆顶值之后，使得剩余n-1个元素的序列重又建成一个堆，则得到n个元素中的次小值。如此反复执行，便能得到一个有序序列。

1. 建堆：用顺序结构存完全二叉树，n个元素只需n个结点
2. 筛选：输出堆顶，即堆顶与堆的最后一个元素交换；再将剩余的元素自堆顶至叶子调整成堆。

图片演示

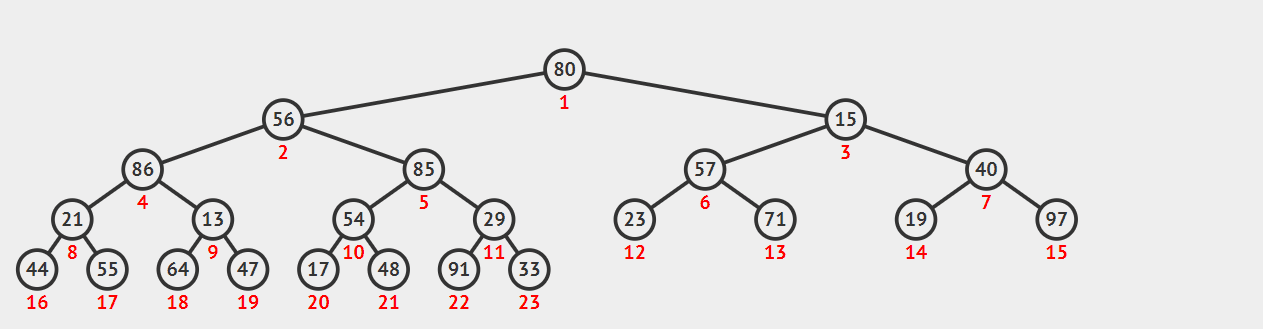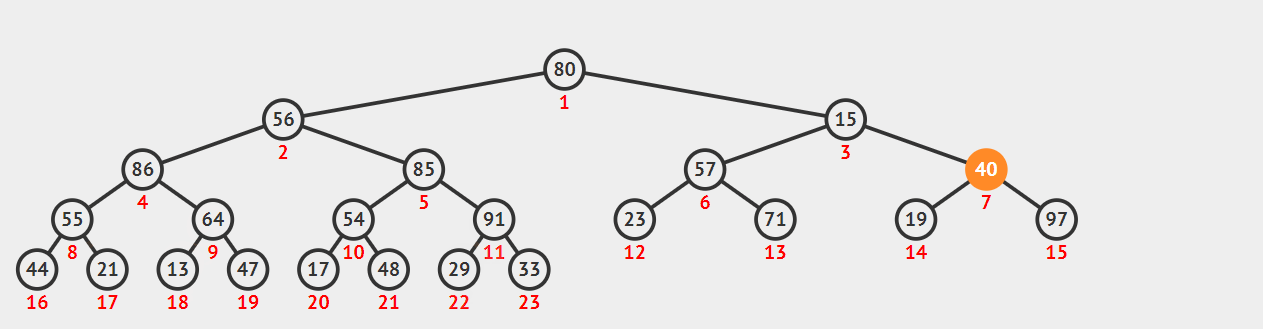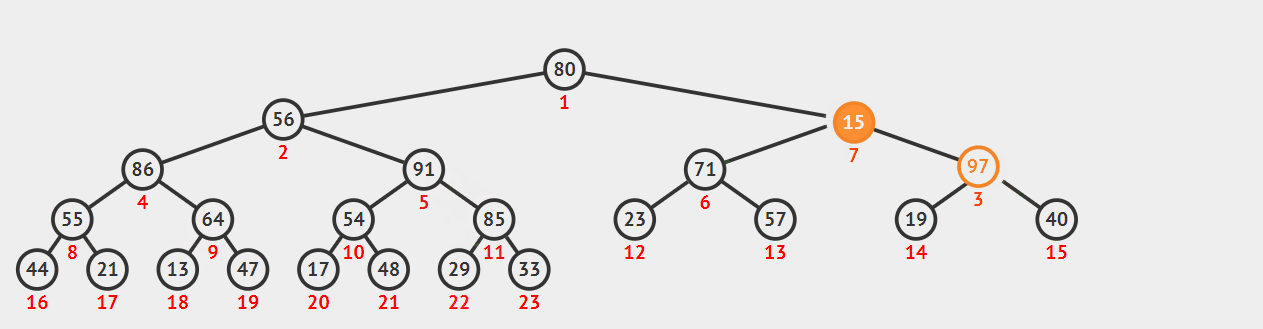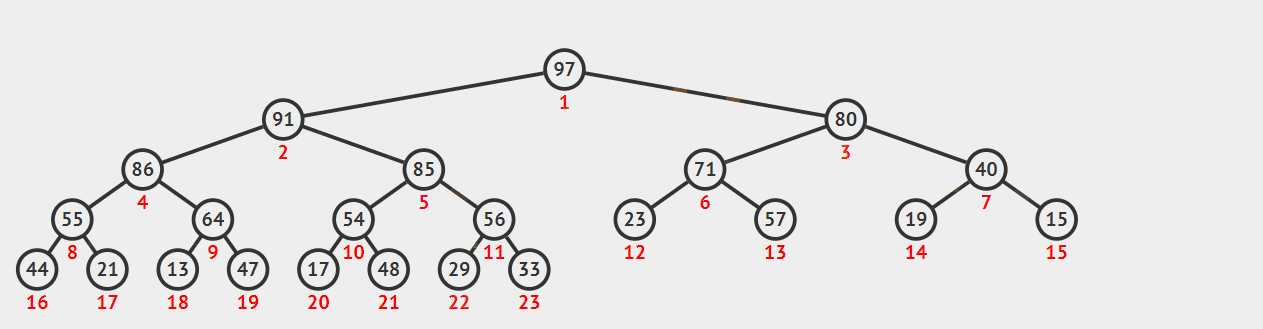
代码

public class Heap {
    /**
     * 找孩子
     *
     * @param i 堆中某项的索引
     * @return 左子结点的索引
     */
    private static int leftChild(int i) {
        return 2 * i + 1;
    }

    /**
     * buildHeap，deleteMax=把最大的放到最后
     *
     * @param a 一组可比较的项目
     * @param i 向下渗透的位置
     * @param n 二叉堆的逻辑大小
     */
    private static <AnyType extends Comparable<? super AnyType>>
    void percDown(AnyType[] a, int i, int n) {
        //1.定义左孩子的索引
        int child;
        //2.定义一个变量存
        AnyType tmp;

        //3.循环建堆，让大的在上面，条件是孩子的索引要小于总节点数
        for (tmp = a[i]; leftChild(i) < n; i = child) {
            //1.找左孩子
            child = leftChild(i);
            //2.找孩子中比较大的
            if (child != n - 1
                    && a[child].compareTo(a[child + 1]) < 0) {
                child++;
            }
            //3.假如双亲小，就跟child交换
            if (tmp.compareTo(a[child]) < 0) {
                a[i] = a[child];
            } else {
                break;
            }
        }
        //4.若上面交换了，a[i]就指向孩子，换回原来的值
        a[i] = tmp;
    }

    /**
     * 交换到数组中的元素
     *
     * @param a      对象数组
     * @param index1 第一个对象的索引
     * @param index2 第二个对象的索引
     */
    private static <AnyType extends Comparable<? super AnyType>>
    void swapReferences(AnyType[] a, int index1, int index2) {
        AnyType tmp = a[index1];
        a[index1] = a[index2];
        a[index2] = tmp;
    }

    /**
     * 标准堆排序
     *
     * @param a 一组可比较的项目
     */
    public static <AnyType extends Comparable<? super AnyType>>
    void heapSort(AnyType[] a) {
        //1.首次建堆，把最大放到顶，递减的i遍历每颗最小子树
        for (int i = a.length / 2 - 1; i >= 0; i--) {
            percDown(a, i, a.length); /* buildHeap */
        }

        //2.替换堆顶，删除最大的。重新建堆，每次少一个点
        for (int i = a.length - 1; i > 0; i--) {
            swapReferences(a, 0, i); /* deleteMax */
            percDown(a, 0, i);
        }
    }

}

分析

时间复杂度为O(NlogN)