思想
基本思想是任取待排序对象序列中的某个对象(三值分割法取得)作为基准,按照该对象的排序码大小,将整个对象序列划分为左右两个子序列:
- 左侧子序列中所有对象的排序码都小于或等于基准对象的值
- 右侧子序列中所有对象的排序码都大于基准对象的值
- 基准对象则排在这两个子序列中间(这也是该对象最终应安放的位置)。
然后分别对这两个子序列重复施行上述方法,直到所有的对象都排在相应位置上为止。
基准对象也称为枢轴(或支点)记录。
演示
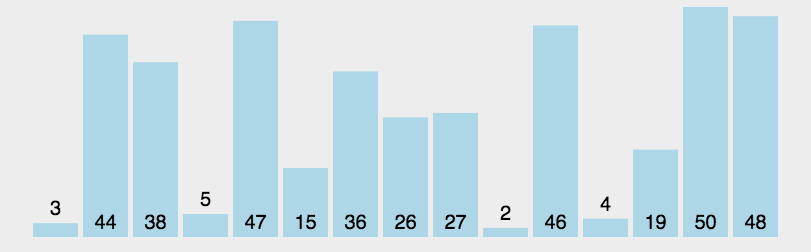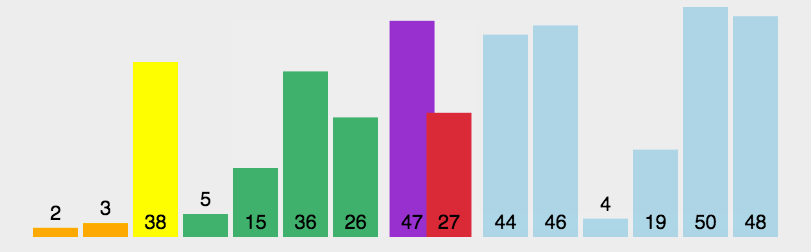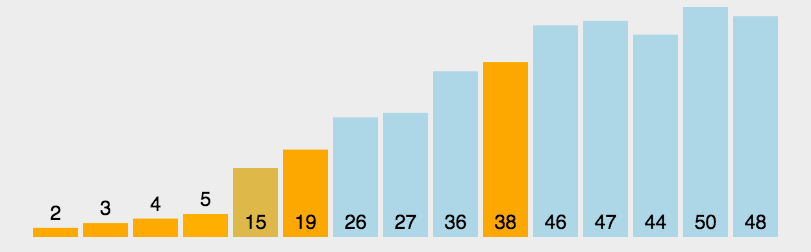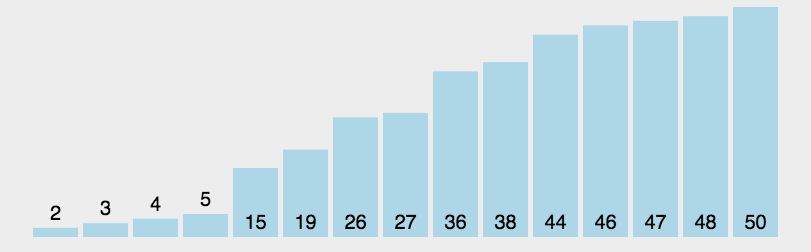
代码
class QuickSort {
fun swap(a: IntArray, i: Int, j: Int) {
val tmp = a[i]
a[i] = a[j]
a[j] = tmp
}
fun median3(a: IntArray, l: Int, r: Int): Int {
val mid = (l + r) / 2
if (a[l] > a[mid]) {
swap(a, l, mid)
}
if (a[l] > a[r]) {
swap(a, l, r)
}
if (a[mid] > a[r]) {
swap(a, mid, r)
}
// 此时: 小。。中。。大
swap(a, mid, r - 1)
// 此时:小。。。。。中, 大
return a[r - 1]
}
fun quickSort(a: IntArray, left: Int = 0, right: Int = a.size - 1) {
// note jin: 至少还有三个元素
if (left + 1 < right) {
// 三值分割法取合适的监视哨
val pivot = median3(a, left, right)
// 分布:小。。。。。中, 大,故只对中间部分排,最后中(pivot)放到中间值位置
var i = left
var j = right - 1
// 循环交换比 pivot 大和小的值, 且确定pivot位置
while (true) {
//1.找比监视哨大的
while (a[++i] < pivot) {
}
//2.找比监视哨小的
while (a[--j] > pivot) {
}
//3.若i<j,说明逆序,要交换,继续找下一对,i>j说明找一轮下来了
if (i < j) {
swap(a, i, j)
} else {
break
}
}
//4.pivot找到正确位置i,此时 i 位置元素比 pivot 大
swap(a, i, right - 1)
//5.pivot左边部分再快排
quickSort(a, left, i - 1);
//6. pivot右边也快排
quickSort(a, i + 1, right);
} else {
// note jin: 两个元素直接交换
if (a[left] > a[right]) {
swap(a, left, right)
}
}
}
}
泛型版
// 交换
private static <T extends Comparable<? super T>>
void swap(T[] a, int i, int j) {
T tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
//三值分割
private static <T extends Comparable<? super T>>
T median3(T[] a, int l, int r) {
int mid = (l + r) / 2;
if (a[l].compareTo(a[mid]) > 0) {
swap(a, l, mid);
}
if (a[l].compareTo(a[r]) > 0) {
swap(a, l, r);
}
if (a[mid].compareTo(a[r]) > 0) {
swap(a, mid, r);
}
// ..小...中,大
swap(a, mid, r - 1);
return a[r - 1];
}
private static <T extends Comparable<? super T>>
void quickSort(T[] a, int left, int right) {
if (left + 1 < right) {
//1.三值分割法取合适的监视哨
T pivot = median3(a, left, right);
//2.定义位置
int i = left, j = right - 1;
//3.循环找pivot位置,交换比 pivot 大和小的值
for (; ; ) {
//1.找比监视哨大的
while (a[++i].compareTo(pivot) < 0) {
}
//2.找比监视哨小的
while (a[--j].compareTo(pivot) > 0) {
}
//3.若i<j,说明逆序,要交换,然后继续找一对。i>j说明找一轮下来了,没有逆序,当前pivot这一轮结束
if (i < j) {
swap(a, i, j);
} else {
break;
}
}
//4.pivot找到正确位置i
swap(a, i, right - 1);
//5.pivot左边部分再快排
quickSort(a, left, i - 1);
//6. pivot右边也快排
quickSort(a, i + 1, right);
} else {
if (a[left].compareTo(a[right]) > 0) {
swap(a, left, right);
}
}
}
public static <T extends Comparable<? super T>> T[] quickSort(T[] a) {
quickSort(a, 0, a.length - 1);
return a;
}
分析
最坏情况,基本逆序:O(n2)
平均情况:O(nlogn)
