拓扑排序

思想

存储：

• 找一个存放入度为零这些点的东西，队列，表都可以。
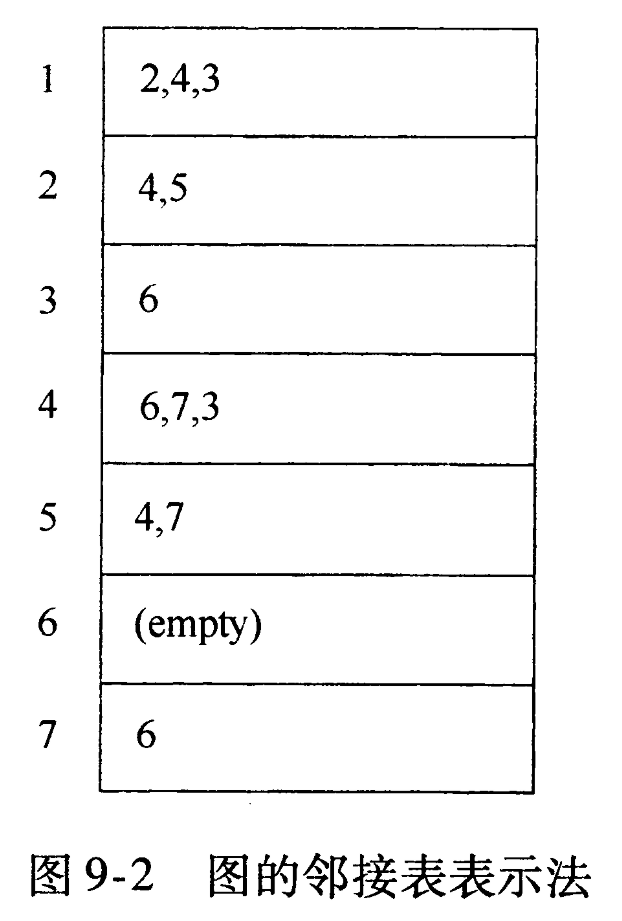
• 一个链表存放点，也就是邻接表。
  

1. 首先，对每个顶点计算它的入度。
2. 然后，将所有人度为0的顶点放人一个初始为空的队列中。
3. 当队列不空时，删除一个顶点v，并将 与v邻接的所有顶点的入度均减1。
4. 只要一个顶点的入度降为0,就把该顶点放人队列中。此 时，拓扑排序就是顶点岀队的顺序。

步骤

1. 定义存放入度为零的顶点的队列
2. 把邻接矩阵换位邻接表
3. 定义出队顺序编号变量
4. 先找一遍所有入度为零的点，放到队列
5. 循环出队，安排出队序号，指向的点入度减一。如果队列空，没有入度为0的，有环
6. 如果序号最大值不等于点数，有环

代码

public class Graph {

    /**
     * 把邻接矩阵转邻接表
     *
     * @param matrix 图的邻接矩阵,点从0开始
     */
    private static List<Vertex<Integer>> adjMatrix2List(Integer[][] matrix) {
        //1. 定义点的列表，要初始化好入度，指向的点，值
        List<Vertex<Integer>> vertexList = new LinkedList<>();

        //2. 遍历每一个点，找其所有adjVertex
        for (int i = 0; i < matrix.length; i++) {
            Integer[] edges = matrix[i];
            Vertex<Integer> vertex = new Vertex<>(i);
            for (int j = 0; j < edges.length; j++) {
                //点有指向这个j点
                if (edges[j] == 1) {
                    vertex.nextVertices.add(j);
                }
            }
            vertexList.add(vertex);
        }

        //3. 统计每个点入度
        for (int i = 0; i < matrix.length; i++) {
            int indegree = 0;
            for (int j = 0; j < matrix.length; j++) {
                //对每一列遍历
                if (matrix[j][i] == 1) {
                    indegree++;
                }
            }
            //对每个点设置入度
            vertexList.get(i).indegree = indegree;
        }
        return vertexList;
    }

    /**
     * 标准拓扑排序
     *
     * @param matrix 图的邻接矩阵,点从0开始.
     * @throws CycleFoundException 有环
     */
    public static List<Vertex<Integer>> topSort(Integer[][] matrix) throws CycleFoundException {
        //1. 定义存放入度为零的顶点的队列
        Queue<Vertex<Integer>> vertexQueue = new LinkedList<>();
        //2.把邻接矩阵换位邻接表
        List<Vertex<Integer>> vertexList = adjMatrix2List(matrix);
        //3. 定义出队的顺序编号
        int counter = 0;
        //4. 找所有入度为零的点
        for (Vertex<Integer> vertex : vertexList) {
            if (vertex.indegree == 0) {
                vertexQueue.add(vertex);
            }
        }

        //5. 出队，安排出队序号，指向的点入度减一。如果队列空，没有入度为0的，有环
        while (!vertexQueue.isEmpty()) {
            //1. 出队，假如随机出来就可以有不同排列
            Vertex<Integer> v = vertexQueue.poll();
            System.out.println("v" + (v.value + 1));
            //2. 指定排序序号数字
            v.topNum = ++counter;
            //3. v出队之后，对每个v指向的点，入度减一。如果减为零，入队
            for (Integer x :
                    v.nextVertices) {
                // 找x对应的点
                for (Vertex<Integer> vertex : vertexList) {
                    if (x.equals(vertex.value)) {
                        // 入度减一，为零则进队
                        if (--vertex.indegree == 0) {
                            vertexQueue.add(vertex);
                        }
                        break;
                    }
                }
            }
        }

        //6. 如果序号最大值不等于点数，有环
        if (counter != vertexList.size()) {
            throw new CycleFoundException();
        }
        return vertexList;
    }

    static class CycleFoundException extends Exception {
    }


    private static class Vertex<AnyType extends Comparable<? super AnyType>> {

        AnyType value;
        int topNum;//出队时排第几
        int indegree;
        LinkedList<AnyType> nextVertices;

        public Vertex(AnyType value) {
            this.value = value;
            this.topNum = 0;
            this.indegree = 0;
            this.nextVertices = new LinkedList<>();
        }
    }
}

测试代码

public class Main {
    public static void main(String[] args) {

        Integer[][] m = {
                {0,1,1,1,0,0,0,},
                {0,0,0,1,1,0,0,},
                {0,0,0,0,0,1,0,},
                {0,0,1,0,0,1,1,},
                {0,0,0,1,0,0,1,},
                {0,0,0,0,0,0,0,},
                {0,0,0,0,0,1,0,},
        };
        try {
            Graph.topSort(m);
        } catch (Graph.CycleFoundException e) {
            System.err.println("发现环");
        }
    }

}

输出

v1, v2, v5, v4, v3, v7, v6,